And visually, all we are doing is calculating the slope of the secant line passing between two points. The rate of change of position is velocity, and the rate of change of velocity is acceleration. Because \(v Because \(v0\), velocity and acceleration are acting in opposite directions. In other words, the particle is being accelerated in the direction opposite the direction in which it is traveling, causing \(|v|\) to decrease. Let \(s\) be a function giving the position of an object at time t.

• As a business owner, this should be encouraging, even with such a decrease in 2008, he still showed a profit over the 24 years in business.
• The following formulas find the slope, or average rate of change, between the points and .
• Alright, so now it’s time to look at an example where we are asked to find both the average rate of change and the instantaneous rate of change.

Predict the future population from the present value and the population growth rate. The average rate of change formula is the same as the formula for slope. The following formulas find the slope, or average rate of change, between the points and . This indicates the speed went down or decreased 15 miles per hour because of the negative sign. Notice the slope on the graph is going ‘downhill’ on this section, which is a decreasing slope and our mph is negative.

Slope and average rate of change is exactly the same thing. Be sure to keep track of the units in both the numerator and denominator. The average rate of change is the rate of speed upon which a variable quantity changes with respect to the variation in another quantity in a defined time. The Average Rate of Change is mainly used when talking about momentum. It may usually be expressed as a quantitative relation between a change occurring in one variable quantity to a corresponding change occurring in another variable.

The rate of change tells us how something changes over time. Apply the formula and substitute the initial and final values of the interval. Ethan has a PhD in astrophysics and is currently a satellite imaging scientist. Sign up to read all wikis and quizzes in math, science, and engineering topics. Your speed might change based on things like different speed limits, traffic, or a decision to speed.

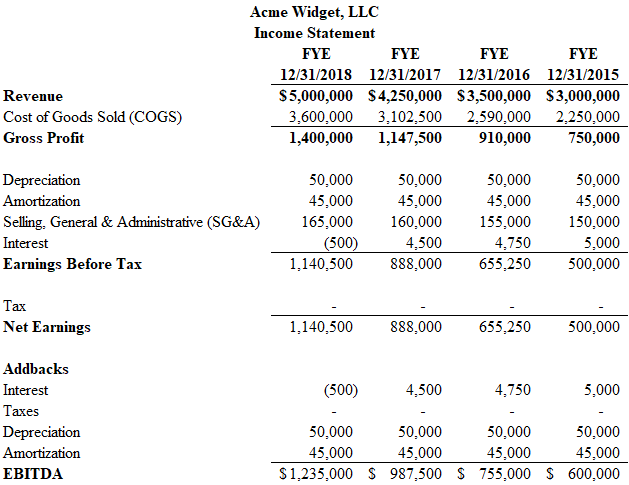
Calculating Average Rate of Change in Excel:

average rate of change formula the average rate of change is a crucial financial concept because this permits the investors to identify security momentum and different trends. For instance, security with high momentum, or one that incorporates a positive Rate of Change, usually outperforms the market in the short term. Conversely, security that includes a rate of change that falls below its moving average or incorporates a low or negative rate of change will probably lessen the value. On the graphs in Figures 1.3.8 and 1.3.9, plot the line segments whose respective slopes are the average rates of change you computed in and . The slope is considered as the average rate of change of a point where the average is taken and is reduced to zero. The slope is the rise over the run which is defined as the average rate of change in y coordinates over the change in x coordinates.

The slope is responsible for connecting multiple points together over a line. The rate of change is easy to calculate if you know the coordinate points. Notice that for part , we used the slope formula to find the average rate of change over the interval. In contrast, for part , we used the power rule to find the derivative and substituted the desired x-value into the derivative to find the instantaneous rate of change.

All we have to do is take the derivative of our function using our derivative rules and then plug in the given x-value into our derivative to calculate the slope at that exact point. Let’s practice finding the average rate of a function, f, over the specified interval given the table of values as seen below. The average rate of change finds how fast a function is changing with respect to something else changing. The marginal revenue is a fairly good estimate in this case and has the advantage of being easy to compute. Apply rates of change to displacement, velocity, and acceleration of an object moving along a straight line. Time is represented on the horizontal axis, and the speed limit represents the vertical axis.

Average Rate of Change Over an Interval

Another way to think of the average rate of change between two points on a plane is the slope of the line connecting the two points. Suppose someone drives their vehicle at 50 mph for an hour. For every one hour driven, the distance the vehicle has traveled increases by 50 miles.

The average rate of change is finding the rate something changes over a period of time. We can look at average rate of change as finding the slope of a series of points. The slope is found by finding the difference in one variable divided by the difference in another variable. The slope formula is used to find the average rate of change. When a function has a negative slope, it means the average rate of change is decreasing.

Average Rate of Change:

Start by replacing the https://1investing.in/ in the average rate of change formula. The formula states that the average rate of change is equal to the result of the function of b f minus the result of the function of a f, divided by the value of b minus the value of a. To find the rate of change, first define the function that you’ll use to calculate it, along with an interval . Find the instantaneous rate of change of the height of water in the cone at time \(t\) (assuming the cone isn’t filled completely yet). An average rate of change is just when you measure how much a function changes across whatever interval you decide . Let’s look at a question where we will use this notation to find either the average or instantaneous rate of change.

The y-values are the dependent variables, and the x-values are the independent variables. If the slope is positive, this is an increasing rate of change. If the slope is negative, this is a decreasing rate of change. We can observe that the Average Rate of Change function is a lot like the formula for finding the slope of a line. When two distinct points are taken on a curve, and , the slope of the line joining the points will be the average rate of change from i1 to i2. Hence, it is derived from the slope of a straight line joining the interval’s endpoints on the function graph.

Another use for the derivative is to analyze motion along a line. We have described velocity as the rate of change of position. If we take the derivative of the velocity, we can find the acceleration, or the rate of change of velocity. It is also important to introduce the idea of speed, which is the magnitude of velocity. Thus, we can state the following mathematical definitions.

So, this means over the course of 24 years, he had an increase of $1,666.67 profit each year. As a business owner, this should be encouraging, even with such a decrease in 2008, he still showed a profit over the 24 years in business. The current through an electrical circuit increases by some amperes for every volt of increased voltage.

It gives an idea of how much the function changed per unit in the given interval. In simple terms, in the rate of change, the amount of change in one item is divided by the corresponding amount of change in another. Let’s look into the average rate of change formula in detail.

To not lose any points in this last step, make sure to note the units that your answer is in! In this case, we wanted to know how much the price of a single lollipop increased over 10 years on average. An interval is a defined range of numbers and what falls in between them. So, if I told you to find the average rate of change between the interval of 2 to 97, you could picture what’s below on a number line or graph. Now, let’s take that and combine it with what a function is.

Joey’s parents are keeping track of Joey’s height as they watch him grow. They notice that he had several growth spurts throughout his first 16 years. The resulting value is the average rate of change of the function.

Give an example of a function that has the same average rate of change no matter what interval you choose. You can provide your example through a table, a graph, or a formula; regardless of your choice, write a sentence to explain. Find the average rate of change by entering a function f and an interval in the calculator below. Where \(\fracyx\) is the instantaneous rate of change of \(y\) with respect to \(x\). It is also called the derivative of \(y\) with respect to \(x\). Calculate the marginal revenue for a given revenue function.

The rate of change function is defined as the rate at which one quantity is changing with respect to another quantity. Let us learn about the rate of change formula with a few examples in the end. If we know the x and y coordinates of the two interval endpoints, we simply use the slope formula to calculate the average rate of change. Using the slope formula saves us time versus using the average rate of change formula. If the value of one coordinate increases significantly but the value of the other coordinate is the same then the rate of change is constant here means it always is the same.

With an ROC model, this is also easy to calculate the growth rate of the population or salary revised rate, etc. With a careful application of ROC mode, you would get to know how applicable it can be to compute the tough problems. With Rate of Change Formula, you can calculate the slope of a line especially when coordinate points are given. The slope of the equation has another name too i.e. rate of change of equation. The population growth rate and the present population can be used to predict the size of a future population.

• In addition to analyzing motion along a line and population growth, derivatives are useful in analyzing changes in cost, revenue, and profit.
• Remember that dividing a negative number by a negative number cancels out the negatives, leaving us with a positive result.
• Instead, it would make more sense to tell someone the average speed we drove to Dallas (aka the average rate of change!).
• For example, the average rate of change in a population of an area can be calculated with only the times and populations at the start and end of the period.

We can use a current population, together with a growth rate, to estimate the size of a population in the future. The population growth rate is the rate of change of a population and consequently can be represented by the derivative of the size of the population. In this section we look at some applications of the derivative by focusing on the interpretation of the derivative as the rate of change of a function. These applications include acceleration and velocity in physics, population growth rates in biology, and marginal functions in economics. As we see here, slope is another version of finding the average rate of change. Average rate of change is finding the difference between the dependent variable (y-term) divided by the difference in the independent variable (x-term).